정규화 (Normalization)
정규화 이론의 목표
- 가능한 데이터 중복성(Redundancy)를 제거해서 한가지 사실은 한 곳에서만 나타난다라는 원칙을 지키도록 한다.
- 즉 정규화 과정(Normalization procedure)란 중복을 최소화하기 위해 데이터를 구조화 하는 작업이다.
- 정규화 과정을 통해 특정 조건을 만족시키는 relation을 정규형이라고 한다. 제 1,2,3…정규형 등이 존재한다.
왜 정규화가 필요한가?
- 정규화를 하지 않는 경우에 data redundancy로 인해 다음과 같은 이상현상들이 발생할 수 있다.
insert annomaly (삼입 이상 ) : 특정 데이터를 삼입하고 싶은데, 자료가 부족해 삼입할 수 없다. 예를 들면 공급자,도시,부품이라는 attribute가 있다고 하면 공급자가 어떤 도시에 살고 있다는 정보는 부품이라는 정보가 있어야만 삼입할 수 있다.
deletion annomaly (삭제 이상) : 하나의 정보를 삭제하고 싶지만, 필요한 정보까지 삭제될 수 있다. 위 예와 동일한데, tuple을 삭제할 경우에 공급자가 어떤 도시에 살고 있다는 정보가 소실될 수 있다.
update annomaly (갱신 이상) : 데이터 갱신 중간 과정에 일부 data는 update된 상태, 일부 data는 original 상태로 inconsistent한 상태가 생길 수 있다.
정규형 만족 조건
- 분해 집합은 무손실 조인, 무손실 분해 (nonloss decomposition)를 만족해야 한다.
- 분해 집합은 함수적 종속성(functional dependency)을 보존해야 한다.
Nonloss Decomposition (무손실 분해) 이란?
- non-loss decomposition : 특정 relation 을 다른 relation으로 분해하는 것으로 , 이 과정은 정보의 손실이 있어서는 안된다. 즉 가역적이여야 한다.
- 가역적이란 말은 분해 이후 다시 table을 join 하였을떄 최초의 relation과 동일해야 한다는 말이다.
Functional Dependency (함수적 종속성) 이란?
- 특정 relation 안에서 하나의 속성 집합에서 다른 속성으로의 다대일 (many-to-one)관계이다. 정확한 정의는 다음과 같다.
R을 relation이라 하고, X와 Y를 R의 속성 집합의 임의의 부분집합이라고 할때, Y가 X에게 함수적으로 종속되기 위한 필요 충분 조건은 다음과 같다. R에 있는 각각의 X의 값이 정확하게 하나의 Y의 값과 관련을 갖는 것이다.이를 “X가 Y를 함수적으로 결정한다.” 또는 기호로는 X->Y 로 표시한다.
예를 들면 아래와 같은 relation에서
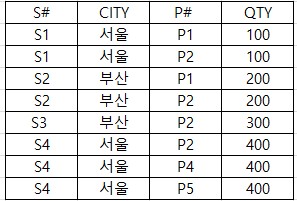
S# -> CITY FD를 만족한다. 그 이유는 CITY가 S#에게 함수적으로 종속되기 위한 필요 충분 조건은 S#의 값이 정확하게 하나의 CITY의 값을 가지는 것인데,
동일한 S# attribute는 동일한 CITY값을 가지기 때문이다.
S# -> CITY 에서 좌변을 결정자(determinant) , 우변을 종속자(dependent)라고 자주 부른다.
- 만일 x가 relation 의 후보키 (candidate key) 라면 반드시 relation의 모든 속성들 y는 x에 함수적으로 종속되어야 한다.
이는 후보키 정의를 보면 당연한데, 후보키 는 다음과 같은 성질을 만족할떄 후보키라고 한다.
- 유일성 : 유일하게 tuple을 식별
- 비분해성 : 해당 후보키의 부분 집합 중에 유일성을 만족시키는 부분집합이 없음
즉 유일성 필요충분조건에 따라 나머지 모든 속성들은 후보키에 함수적으로 종속될 수 밖에 없다.
제 1 정규형
- 어떤 relation 이 1NF 이기 위해서는 모든 attribute가 domain에 속하는 단 하나의 값만을 가져야 한다. 즉 대부분의 relation은 1NF를 대부분 만족한다
제 2 정규형
- 모든 non-key attribute가 primary key에 대해 최소성으로 종속적이다. 즉 기본키에 대해서 나머지 attribute들이 종속적이라는 말이다.
- 완전 함수적 종속이라고도 표현한다.
- 제 2 정규형을 만족시키기 위해서는 기본키에 대해 비최소성을 가지는 함수적 종속성을 제거하면 된다.
제 3 정규형
- 2NF를 만족함과 동시에, 모든 non-key attribute과 primary key에 대해 비이행적(non-transitive dependency)으로 종속적이다.
- 제 3 정규형을 만족시키기 위해서는 기본키를 제외한 non-key attribute간에 상호 종속성을 제거하면 된다.
ex) 예를 들면 기본키인 S# attribute가 있을떄, S# 에 의해 나머지 두 attribute (city,status) 가 최소성으로 종속적이다. 2NF를 만족하는데, city에 의해 status attribute가 결정된다. 즉 이행적 종속관계가 있다는 말이다.
해당 relation의 FD를 정의하면 다음과 같을 것이다.
- s# -> city
- s# -> status
- city -> status
여기서 S#->city->status 임으로 s# -> status 임은 유추될 수 있는 이행적 함수 종속성임으로 제거될 수 있는 FD이다. 따라서 이를 decomposition하여 2개의 relation으로 나누어야 한다. 예를 들면 r1(s#,city) , r2(city,status) 로 2개의 relation으로 나누어질 수 있을 것이다.
BCNF (Boyce/Codd Normal Form) 정규형
- BCNF 정규형이 왜 나왔는가?
이전 3 NF 까지는 후보키가 둘 이상이고, 두 후보키가 복합속성이면서 일부 속성이 겹치는 경우에 데이터 중복이 생기는 현상을 다루지 못했다.
- 비직관적 (non-trivial) , 좌변-최소성(left-irreducible) FD들이 후보키를 결정자로 갖는 것이다. 즉 relation이 BCNF 정규형을 만족시키는 필요충분조건은 오직 후보키들만이 결정자가 되는 것이다.
- 종속성 다이어그램에서 화살표가 후보키에서만 나오는 것이라고 보면 된다.
이외에도 고등 정규형 4NF,5NF가 있는데, 대체로 3NF,BCNF 까지 정규화를 수행한다고 한다. 고등 정규형 4NF,5NF에 대해서는 별도로 정리하여 다루도록 하려고 한다.
정규화 정리
정규화 과정의 목적은 Data 중복성을 제거해 여러가지 이상현상(삼입,삭제,갱신 이상) 현상들을 제거 하고, 실세계에 가깝게 데이터베이스를 설계해서 직관적으로 이해되고 , 확장이 쉬운 구조로 만드는 것이다.
역정규화 (Denormalization)
- 정규화 과정의 성능적인 이슈
정규화 과정을 거치면서 하나의 relation을 물리적으로 여러개의 relation 으로 분해가 이루어진다. 즉 I/O작업이 이루어질떄는 원하는 데이터를 가져올때 그만큼 많은 JOIN연산이 이루어질 수 있다. 따라서 성능적으로 이점을 얻고자 일부 데이터 중복을 허용하면서 JOIN 연산을 피하는 것이 역정규화이다.